博弈树（转载)

什么是博弈树

　　博弈树是指由于动态博弈参与者的行动有先后次序，因此可以依次将参与者的行动展开成一个树状图形。^[1]

　　博弈树是扩展型的一种形象化表述。它能给出有限博弈的几乎所有信息。其基本构建材料包括结、枝和信息集。结包括决策结和终点结两类；决策结是参与人采取行动的时点，终点结是博弈行动路径的终点。枝是从一个决策结到它的直接后续结的连线(有时用箭头表述)，每一个枝代表参与人的一个行动选择。博弈树上的所有决策结分割成不同的信息集。每一个信息集是决策集集合的一个子集，该子集包括所有满足下列条件的决策结：(1)每一个决策结都是同一参与人的决策结；(2)该参与人知道博弈进入该集合的某个决策结，但不知道自己究竟处于哪一个决策结。^[2]

博弈树的特点^[3]

　　(1) 博弈的初始格局是初始节点。

　　(2) 在博弈树中，"或"节点和"与"节点是逐层交替出现的。自己一方扩展的节点之间是"或"关系，对方扩展的节点之间是"与"关系。双方轮流地扩展节点。

　　(3) 所有自己一方获胜的终局都是本原问题，相应的节点是可解节点；所有使对方获胜的终局都认为是不可解节点。

博弈树案例分析^[4]

案例一、软件博弈

　　(1)软件博弈

　　考虑下面的策略局势：计算机软件商宏软公司正决定利用什么样的营销策略推销其新近开发的计算机游戏软件。在经过许多研究后，该公司把它的选择减少为两个：(1)A计划；(2)B计划。宏软公司知道计算机游戏软件的总销售量不会受到选择的广告计划的影响，但这些销售量的时序会非常不同。只要宏软公司是游戏的唯一提供者，使用么计划在第一年的销售量非常高，这是么计划“闪电战”的结果，但在第二年销售量非常小，因为市场接近饱和。B计划第一年的销售量相对小，但第二年的销售量很大，因为早先的用户告诉他们的朋友这个游戏是如何的好。在两个广告计划中，第二年后没有进一步的销售量。

　　因为市场完全饱和。两种计划下每年获得的净利润如表1所示：

　　以表1为基础，显然宏软公司的最优决策是利用比较廉价的B计划，并依赖于博弈在第二年销售量的提高而产生的声誉。但是这一结论忽略了与合法复制宏软游戏软件的潜在竞争者的竞争。计算机游戏软件的合法复制是模仿第一个游戏软件的第二个游戏软件，但它的复制完全不同处在于复制的所有者不能受到侵犯版权的控告。然而，对于宏软公司而言，中软公司拥有生产宏软游戏的法定复制的技术能力，在开始博弈的那一年成本为300000美元。如果中软公司生产复制品，则两个企业会在第二年分割市场。这一假设不考虑其他策略问题，如两个企业在第二年进行价格竞争。表2和表3列出了宏软和中软公司在中软公司进入市场时的利润。显然B计划依然是最优的。

　　由于两个公司的相互依赖性，宏软公司和中软公司在玩一个博弈。为了分析这个博弈，我们需要知道局中人可利用的策略和他们彼此采用这些策略时的得益。构造可能的策略列表的第一步是列出两个局中人可用的行动。宏软公司有两个行动供选择：(1)采用A计划；(2)采用B计划。中软公司也有两个行动供选择：(1)复制游戏软件进入市场；(2)不复制游戏软件不进入市场。我们称这两个行动为进入和不进入。如果这是一个静态博弈，每个局中人的策略集合等价于他们的行动集合。但这不是静态博弈。在这个博弈中，宏软公司先行动，中软公司在做出其进入决策前知道宏软公司的行动。描述这个博弈进行的时序的最简单方法是说宏软公司是先行动者，中软公司是后行动者。因为这一博弈顺序，中软公司可把其行动建立在宏软公司的行动之上。因此中软公司的一个策略，是要说明如果宏软公司采用A计划中软公司将采取什么行动；如果宏软公司采取B计划，中软公司将采取什么行动。这两个不必相同。

　　(2)博弈树

　　为了决定每个企业的策略集合，我们不仅要仔细阐明局中人的行动，而且要阐明这些行动的顺序和他们在做出决策时已有的信息。组织这一信息的强有力的方法是博弈树。博弈树是由结和枝组成的图。博弈树中每个结点代表局中人之一的决策点，该局中人属于在该点行动的局中人。决策结用方框表示，框内是在该结点行动的局中人的名字。一个枝代表局中人一个可能的行动。每个枝连接的两个结点有一个方向。该方向用箭头表示。如果一个枝从结点属于局中人A的结点N_1到属于局中人B的结点N_2，则局中人A在局中人B前行动，结N₁，在终点结N₂前。在本书中，博弈树将总是从顶到底或从左到右进行的。

　　图1是软件博弈的博弈树。该博弈从图的最左边开始，其中宏软选择为其新产品的广告宣传。两个枝从左向右，每个枝代表选择的广告计划。代表的行动被列入枝的上边。每个枝点表示中软公司的一个决策结，因为这个企业在其知道宏软公司已经采用的广告类型后做出其进入决策。从决策结向代表中软公司可能选择的行动的两个枝延伸。这四个箭头的末端是圆点，叫做终点结。在终点结，博弈结束。终点结的右边是两个数字。第一个数字是先行动者(宏软公司)的得益，第二个数字是后行动者(中软公司)的得益。博弈树与所有终点结的得益一起，构成博弈的扩展形式。

　　为了避免模棱两可，博弈树必须遵循四个法则。

　　博弈树法则1 每个结点前至多有一个其他结点直接相联系。

　　图2左边是违背法则1的博弈树。局中人B有两个决策结，从他们的枝到达相同的终点结。如果局中人A的行动对得益没有影响，则该局中人的决策结会因前后不一致而被剔除。而且，如果局中人B的行动对得益有影响，则在博弈树上需要加上两个终点结，对应着A的每个行动。

　　当法则1被满足时，讲一个决策结“跟在另一个决策结后”才有意义。如果从A开始，局中人可能做出后续的行动，使得博弈到结点B，结点B是结点A的后续结。正式地，结点B是结点彳的后续结，当且仅当存在某些后续结N_l,N₂，…，N_K，使得A=N₁，B=N_K，且每个结点直接位于后面的另一个结点之前。这一结点顺序称之为从A到B的路径。法则l意味着在任意两个结点之间至多有一条路径。我们将说结点A是结点B的前列结，当且仅当结点B是A的后续结。终点结没有后续结，初始结没有前列结。称没有终点结的结点为决策结。

　　图3左边是满足博弈树法则1的一个博弈树，但其中有一个“环”：如果局中人A选择“下”，则局中人B开始行动；而且如果局中人B选择“左”，则局中人A开始行动。因此，谁先行动呢?为了剔除此种任意性，我们将避免有环状的决策树。图3右边的博弈树是正确的：局中人A行动两次，一次在局中人B之前，一次在局中人B之后。

　　博弈树法则2 在一个博弈树中不能有路径把一个决策结与其自身相联结。

　　图4是满足博弈树法则1和2的博弈树，但没有初始结。然而，“无头”的决策结有可能产生某些策略组合后果的任意性。由于这个原因，我们需要决策树满足法则3。

　　博弈树法则3 每个结是一个唯一初始结的后续结

　　博弈树法则1、2和3意味着每个结点在其前列结中只有一个初始结。但是，整个博弈树可能有一个以上的初始结。不过，不管这在何时发生，结点都可根据他们在哪个初始结之后被分成不连续的集合。我们要求这些不连续的结点子集(和联结他们的枝)的每个可被看成是满足博弈树法则1、2、3的分离的博弈树。而且这每一个“子树”，根据构造只有一个初始结(如图5所示)。在图5中，博弈树有一个以上初始结的任何博弈都可以分成彼此独立的博弈，每个独立的博弈只有一个初始结。我们称这个唯一的初始结是博弈树的根。因此，不失一般性，最后要求满足博弈树法则4。

　　博弈树法则4 每个博弈树只有一个初始结

　　(3)策略

　　策略是局中人进行博弈的详细计划集合。局中人的一个策略必须说明在该局中人的每一个决策结所采取的行动。因为宏软公司只有一个决策结，所以宏软公司的策略就只包括其选择两个行动之一。中软公司有两个决策结。中软公司的一个策略是基于宏软公司先前的广告选择，在进入或不进入市场间决策。中软公司的一个可能的策略是：如果宏软公司采用A计划，中软公司就进入，如果宏软公司采用B计划，中软公司就不进入。我们把这一策略写成：(进入，不进入)。第一部分即进入，描述了如果宏软公司采用A计划，中软公司将采取的策略；第二部分不进入描述的是，如果宏软公司采用的是B计划，中软公司所采取的策略。这是四个可能的策略之一。其他三个策略，请读者写出。策略和行动容易混淆。关键是要理解策略不同于行动。策略所刻画的是在所有可能的事件下的计划。不同的策略可产生相同的行动顺序，例如，中软公司和宏软公司博弈中的下面两个策略组合：{B计划，(不进入，进入))，{A计划，(进入，不进入))。

　　(4)信息

　　如果一个局中人知道在他开始行动时博弈进行到哪里，则就说该局中人有完美信息。如果博弈的每个局中人都有完美信息，该博弈就是完美信息动态博弈。多数博弈，如下象棋或者下跳棋，是完美信息博弈。软件博弈1是一个完美信息博弈。此外，一个局中人在不知道另一个局中人先前的行动时必须行动，此局中人就有不完美信息。如果至少有一个局中人有不完美信息，该搏弈就是不完美信息博弈。静态博弈是不完美信息博弈，如多数纸牌游戏。

　　(5)结果和得益

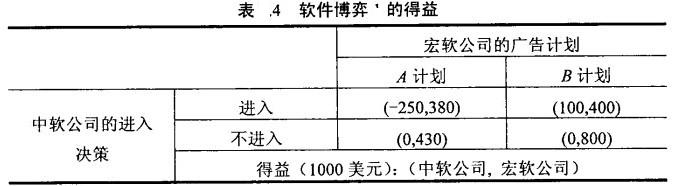
　　软件博弈中宏软公司和中软公司的得益如表4所示。宏软公司的行动和策略是一致的，而中软公司的行动与策略不一致。表4列出了中软公司的行动而不是其策略。表4告诉我们，如果宏软公司选择爿计划，中软公司就选择进入，则宏软公司将获得380000美元的利润，中软公司将承受250000美元的亏损。