最小生成树-Prim算法和Kruskal算法

Prim算法

1.概览

普里姆算法（Prim算法），图论中的一种算法，可在加权连通图里搜索最小生成树。意即由此算法搜索到的边子集所构成的树中，不但包括了连通图里的所有顶点（英语：Vertex (graph theory)），且其所有边的权值之和亦为最小。该算法于1930年由捷克数学家沃伊捷赫·亚尔尼克（英语：Vojtěch Jarník）发现；并在1957年由美国计算机科学家罗伯特·普里姆（英语：Robert C. Prim）独立发现；1959年，艾兹格·迪科斯彻再次发现了该算法。因此，在某些场合，普里姆算法又被称为DJP算法、亚尔尼克算法或普里姆－亚尔尼克算法。

2.算法简单描述

1).输入：一个加权连通图，其中顶点集合为V，边集合为E；

2).初始化：V_new = {x}，其中x为集合V中的任一节点（起始点），E_new = {},为空；

3).重复下列操作，直到V_new = V：

a.在集合E中选取权值最小的边<u, v>，其中u为集合V_new中的元素，而v不在V_new集合当中，并且v∈V（如果存在有多条满足前述条件即具有相同权值的边，则可任意选取其中之一）；

b.将v加入集合V_new中，将<u, v>边加入集合E_new中；

4).输出：使用集合V_new和E_new来描述所得到的最小生成树。

下面对算法的图例描述

图例	说明	不可选	可选	已选（Vnew）
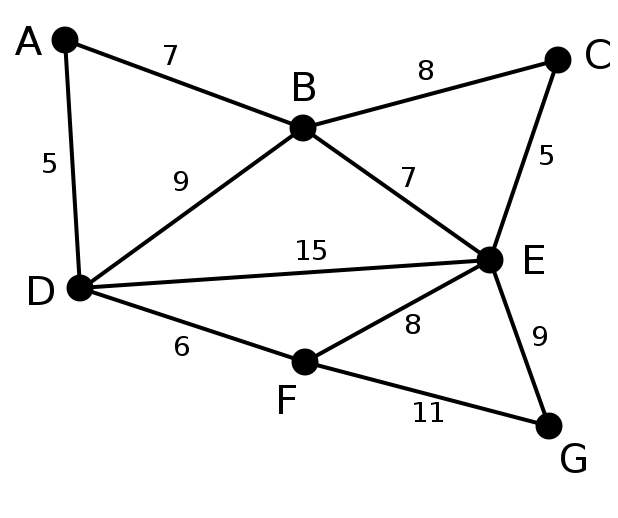
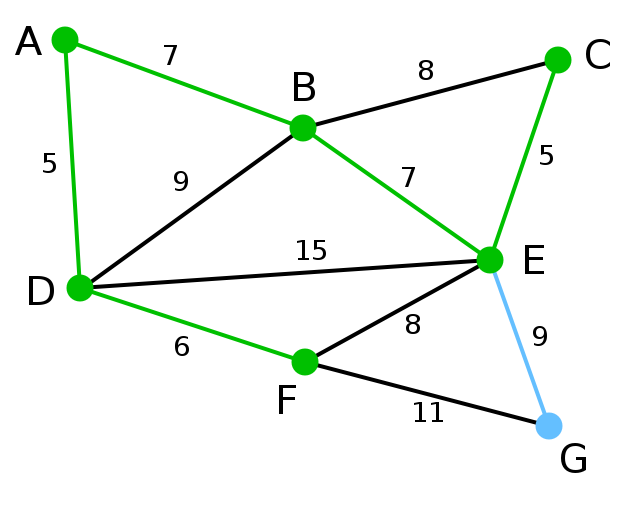
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
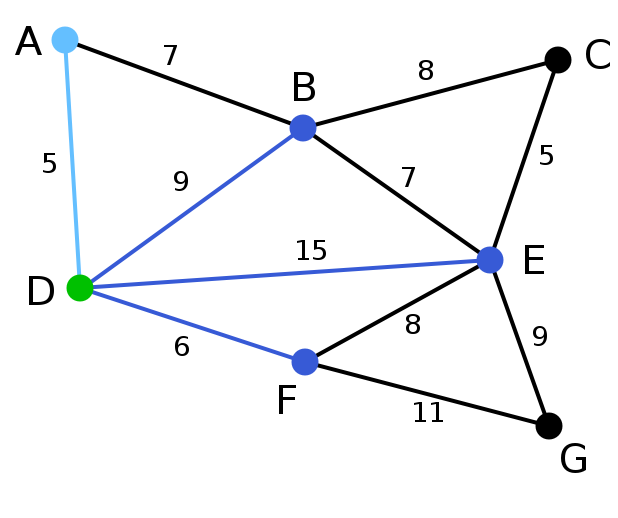
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
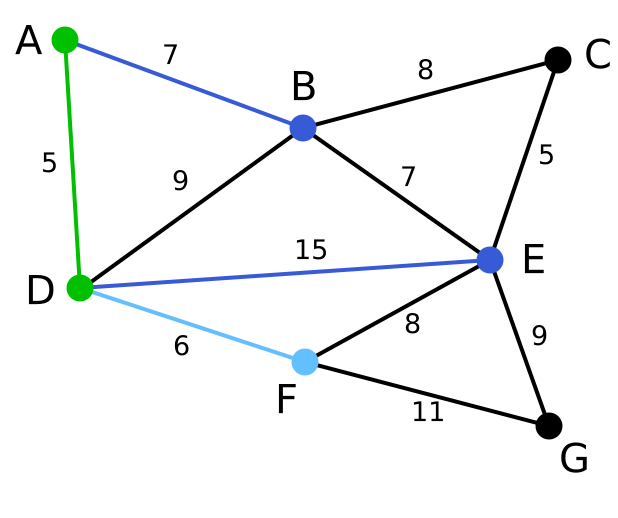
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
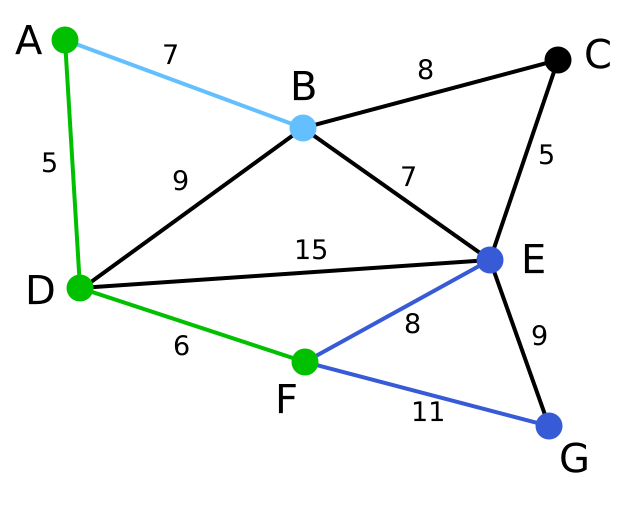
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C
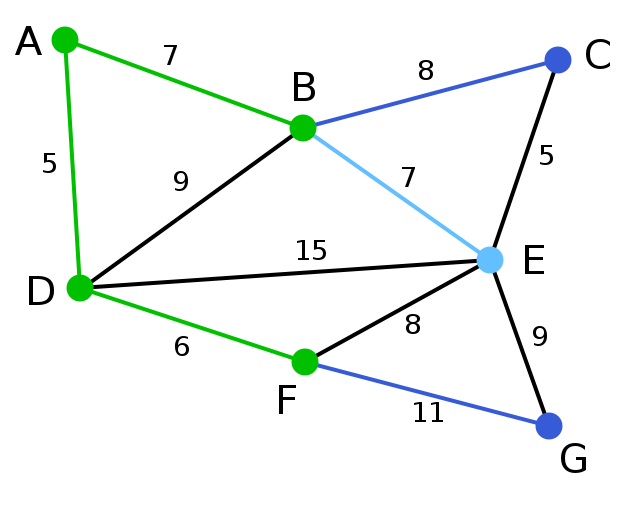
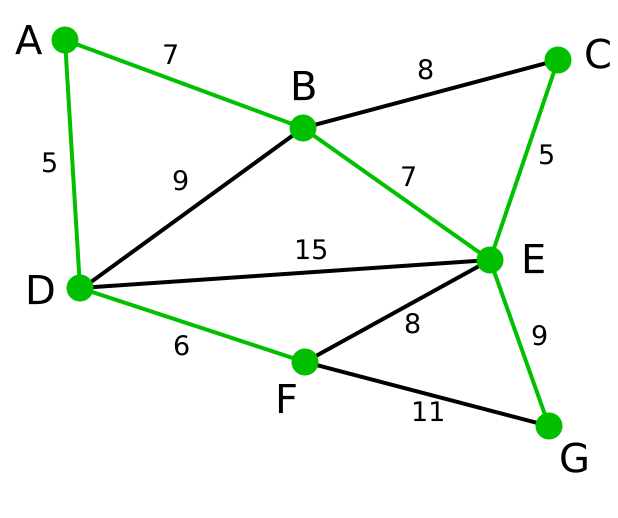
	现在，所有顶点均已被选取，图中绿色部分即为连通图的最小生成树。在此例中，最小生成树的权值之和为39。	无	无	A, D, F, B, E, C, G

定义一个图

GraphArr = [
                    [0, 6, 1, 5, MAX_NUM, MAX_NUM],
                    [6, 0, 5, MAX_NUM, 3, MAX_NUM],
                    [1, 5, 0, 5, 5, 4],
                    [5, MAX_NUM, 5, 0, MAX_NUM, 2],
                    [MAX_NUM, 3, 6, MAX_NUM, 0, 6],
                    [MAX_NUM, MAX_NUM, 4, 2, 6, 0],
                 ]        

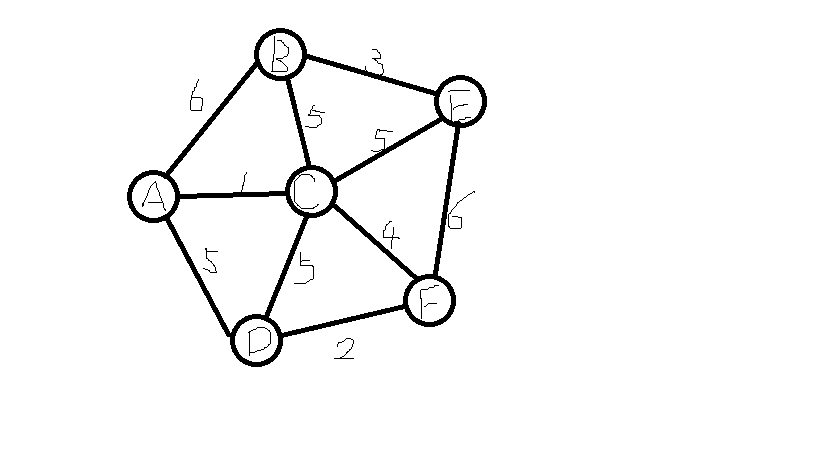
PS：画的不是很好 哈哈 意思是这样子的

'''
最小生成树 prim算法
普里姆（Prim）算法：由线到点，适合边稠密。时间复杂度O(N^2)
'''

Debug_P = 0
V_NUM   = 6
MAX_NUM = 10000

GraphArr = [
            [0, 6, 1, 5, MAX_NUM, MAX_NUM],
            [6, 0, 5, MAX_NUM, 3, MAX_NUM],
            [1, 5, 0, 5, 5, 4],
            [5, MAX_NUM, 5, 0, MAX_NUM, 2],
            [MAX_NUM, 3, 6, MAX_NUM, 0, 6],
            [MAX_NUM, MAX_NUM, 4, 2, 6, 0],
           ]

# U放已经匹配好的顶点:
U = []
# V初始化为所有顶点的集合:
V = []
# T放各个边:
T = []

def init():
    if(Debug_P):
        print("GraphArr = ", end = "")
        print(GraphArr)
    i = 0
    while i < V_NUM:
        V.append(i+1)
        i = i+1

def prim_start_vertex(start):
    if(start < 1):
        print("ERROR: start = ", start)
        print("ERROR: change start to 1 by default")
        start = 1

    U.append(start)
    del V[start-1]

def list_sort(list):
    if(len(list) < 1):
        print("ERROR: Len Of List = ", len(list))
        exit(1)

    index = 0
    i = 0
    min_val = list[0]
    while i < len(list):
        if min_val > list[i]:
            min_val = list[i]
            index = i
        i = i+1
    if(Debug_P):
        print("[list_sort]: list = ", list, ", index = ", index)
    return index


def min_wui():
    m = MAX_NUM
    close_edge = {'u':-1, 'v':-1}
    edge_list = []
    vertex_list = []
    i = 0
    j = 0

    # 算出U和V之间所有边的长度:
    lu = len(U)
    lv = len(V)
    if(Debug_P):
        print("########### entry min_wui ###########")
        print("lu = ", lu,", lv = ", lv)
    while i < len(U):
        while j < len(V):
            if(Debug_P):
                print("i = ", i, "j = ", j)
                print("U[i] = ", U[i], ", V[j] = ", V[j])
            temp = GraphArr[ U[i]-1 ][ V[j]-1 ]
            if(temp > 0):
                if(temp < MAX_NUM):
                    close_edge = {'u':U[i], 'v':V[j]}
                if(Debug_P):
                    print("close_edge = ", close_edge)
                vertex_list.append(close_edge)
                edge_list.append(temp)
            j = j+1
        i = i+1
        j = 0
    if(Debug_P):
        print("vertex_list = ", vertex_list)
        print("edge_list = ", edge_list)
    min_index = list_sort(edge_list)
    close_edge = vertex_list[min_index]
    U.append(close_edge['v'])
    del V[V.index(close_edge['v'])]
    if(Debug_P):
        print("U=",U)
        print("V=",V)
    return close_edge


def py_prim(start):
    init()
    prim_start_vertex(start)
    print("init values:")
    print("U = ", U)
    print("V = ", V)
    print("T = ", T)

    while(len(U) != V_NUM):
        if(Debug_P):
            print("len(U) = ", len(U))
        our_edge = min_wui()
        T.append(our_edge)
    print("========RESULT============")
    print("U=",U)
    print("V=",V)
    print("T=",T)

if(__name__ == '__main__'):
    Debug_P = 1
    py_prim(1)